|
Конические кривые |
Scroll |
Конические кривые или кривые конических сечений — плоские кривые линии, получаемые при пересечении прямого кругового конуса с плоскостями, различно расположенными по отношению к оси конуса.
Существуют три типа конических сечений:
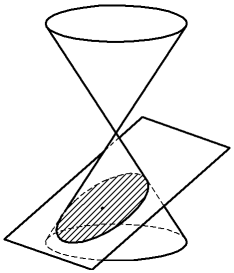
•Секущая плоскость пересекает все образующие конуса в точках одной его полости; линией пересечения является замкнутая кривая — эллипс (рисунок а). Окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса. Если плоскость проходит через вершину конуса, не пересекая при этом ни одной его полости, окружность вырождается в точку.
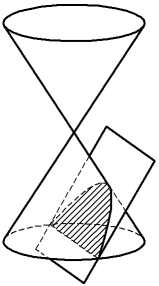
•Секущая плоскость параллельна одной из образующих конуса; в сечении получается незамкнутая, уходящая в бесконечность кривая — парабола, целиком лежащая на одной полости конуса (рисунок б). Если плоскость касается поверхности конуса по образующей, парабола вырождается в две совпавшие прямые.
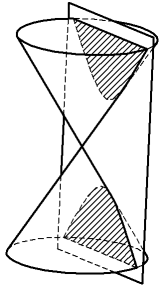
•Секущая плоскость пересекает обе полости конуса; линия пересечения — гипербола — состоит из двух незамкнутых уходящих в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса (рисунок в). Если секущая плоскость проходит через ось конуса, гипербола вырождается в две пересекающиеся прямые.
|
|
|
а) |
б) |
в) |
Конические сечения: а) эллипс, б) парабола, в) гипербола
В алгебраических терминах конические сечения определяются как плоские кривые, координаты которых в декартовой системе координат удовлетворяют уравнению второй степени. Уравнение всех конических сечений можно записать в общем виде как
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
Знак дискриминанта B2 - 4AC определяет тип конического сечения:
•если дискриминант меньше нуля, то это эллипс (или точка),
•если дискриминант равен нулю, то это парабола (или прямая),
•если дискриминант больше нуля, то это гипербола (или пара пересекающихся прямых).
В параметрическом виде коническая кривая может быть представлена уравнениями:
•парабола
x = t
y = a * t2 + b * t + c
-∞ < t < +∞
•гипербола
•левая ветвь
x = -a * (et + e-t) / 2
y = b * (et - e-t) / 2
-∞ < t < +∞
•правая ветвь
x = a * (et + e-t) / 2
y = b * (et - e-t) / 2
-∞ < t < +∞
•эллипс
x = a * cos (t)
y = b * sin (t)
0 < t < 2π
|
Параметрические уравнения конических кривых могут быть использованы для их построения с помощью команды Кривая по закону (см. раздел Кривая по закону). Эти уравнения доступны в разделе Законы диалога Вставка математического выражения. |
При графическом построении коническая кривая может быть задана произвольным набором n своих точек и m касательных, при условии, что n + m = 5. Один из наиболее употребительных способов задания конической кривой — задание ее двумя касательными, точками касания на них и коэффициентом k (инженерным дискриминантом).
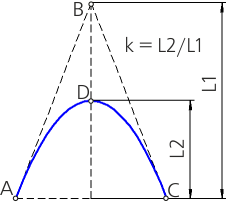
Коэффициент k (инженерный дискриминант) — отношение части медианы треугольника АВС, расположенной под кривой, к полной величине медианы треугольника (рисунок а).
Для параболы значение коэффициента k равно 0,5.
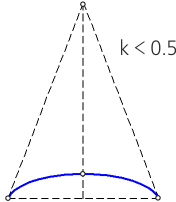
Для эллипса значение k больше 0, но меньше 0,5 (0 < k < 0,5).
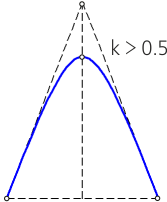
Для гиперболы значение k больше 0,5, но меньше 1 (0,5 < k < 1).
|
|
|
а) |
б) |
в) |
Зависимость типа конической кривой от величины коэффициента
а) парабола; б) эллипс; в) гипербола
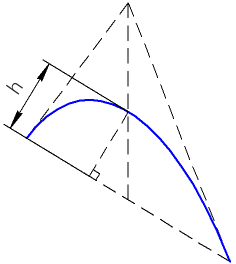
Точка пересечения конической кривой с медианой треугольника может быть задана высотой.
Высота h конической кривой — расстояние от точки пересечения кривой с медианой треугольника до стороны, к которой проведена медиана (рисунок ниже).
|
Высота конической кривой