|
Conditions for curves and surfaces mating |
Scroll |
The mating condition determines the shape of the curve or the surface created near its junction with the existing curve or surface. Such existing curve or surface is referred to as the mating object in relation to the created curve or surface. Curves are mated with each other and with surfaces at the mating point, while surfaces are mated along the curve referred to as the mating boundary.
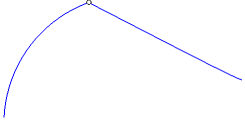
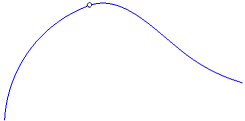
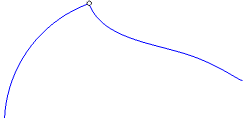
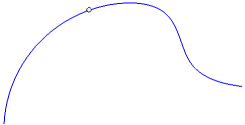
The result of the mating of curves and surfaces with various mating conditions is described in the table. The table also shows examples of joining curves with different mating conditions. In the left part of the figures there is a curve — a mating object, and in the right part there is a mated curve; the mating point is indicated by a circle.
Conditions for curves and surfaces mating
Mating condition |
Result of mating |
|
|
Not specified The end point of the curve or the boundary of the surface belongs to the mating. |
|
|
By tangent Not specified condition is fulfilled. Besides, the following condition is fulfilled: •for a curve: at the mating point, the curve and the mating object have a common tangent (if the mating object is a surface, then for mating, it is additionally specified a curve lying on this surface and passing through the mating point), •for a surface: at the points of the mating boundary, the isoparametric curves of the mated surface and mating surface have a common tangent. |
|
|
Perpendicular Not specified condition is fulfilled. Besides, the following condition is fulfilled: •for a curve: at the point of mating, the tangents of the curve and the mated object are perpendicular, •for a surface: at the points of the mating boundary, the tangents to the isoparametric curves of the mated surface and mating surface are perpendicular. |
|
|
Smooth By tangent condition is fulfilled. Besides, the following condition is fulfilled: •for a curve: at the point of mating the curvature of the curve is equal to the curvature of the mated object (if the mating object is a surface, an additional curve lying on this surface and passing through the point of mating is specified for the mating), •for a surface: at the points of the mating boundary, the isoparametric curves of the mated surface and mating surface have the same curvature. |
|
|
In some 3D modeling systems, the mating of curves or surfaces under the condition Not specified is called "G0 continuity mating," Tangential — "G1 continuity mating," Smooth — "G2 continuity mating. |