KOMPAS-3D v23

The curvature of the curve at the point M is a quantity characterizing the deviation of the curve in the vicinity of the point from the tangent line at this point.

The curvature of the curve at the point M can be determined with the help of a circle contacting it at this point.

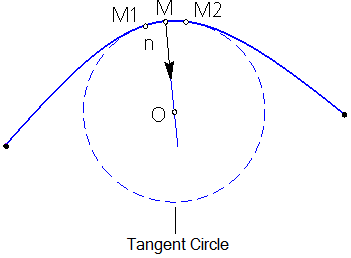
A tangent circle is defined as the limiting position of a circle when it passes through point M and two other points M1 and M2 that are infinitesimally close to it (see figure). The osculating circle lies in the osculating plane of the curve at point M (for osculating plane see section). Basis vectors at a curve point Add-Ons Curves and Surfaces).

Osculating circle at point M of the curve

The center of the circle in contact with the curve at the point M is the center of curvature (O) of the curve at this point, and the radius of this circle is the radius of curvature R of the curve at this point.

The radius of curvature (R) is the quantity that is reciprocal to the curvature (K): R=1/K.

The center of curvature of the curve is always on the principal normal.

The curvature of the surface at point M is a value characterizing the deviation of the surface from the plane.

Various planes pass through the normal at this point M. Sections of the surface with these planes are called normal sections and curvatures of normal sections at the M point are called normal curvatures of the surface at this point. The maximal and minimal normal curvatures at this point M are called the main curvatures.