|
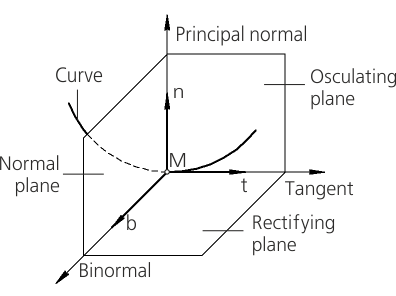
Basis vectors at a curve point |
Scroll |
Three mutually perpendicular planes are connected with each point of the curve: normal, osculating and rectifying planes, as well as three mutually perpendicular basis vectors: tangent t, principal normal n and binormal b.
|
Basis vectors at a curve point
The tangent vector and the principal normal vector lie in the osculating plane, while the binormal vector is perpendicular to that plane.
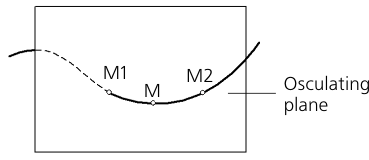
A contacting plane is a plane striving to take the position of a plane passing through three points of a curve M, M1, M2, provided that points M1 and M2 are striving towards point M (see the figure).
|
The plane in which the tangent vector and the binormal vector lie is the rectifying plane, while the plane in which the principal normal vector and the binormal vector lie is the normal plane.