|
3. Spline curves and surfaces. Order of curves. Weight of the points |
Scroll |
Spline curves and surfaces constructed using non-uniform rational B-splines (NURBS) are defined by the following parameters: set of points and order.
When building a curve, the points can be specified arbitrarily; to create a surface, the set of points should represent a grid built over the parametric surface area. The grid is formed by rows of points with the same number of points in each. The series of the grid follow two directions: U and V. Isoparametric curves of the future surface will pass along these rows.
A spline curve or surface may pass through all specified points or only through the extreme points. In the latter case, the points are called poles, and the curve or surface passes at some distance from them. The distance is defined by the weight of each pole.
Obviously, the shape of a spline curve or surface is determined by the spatial location of the points. Surfaces constructed from points possess a very useful property for modeling, namely local deformation: when the position of one point is changed, only the shape of the part of the surface near this point changes, not the entire surface.
The spline degree for a curve is equal to the maximum order of the polynomials describing the parts of this curve +1.
The degree value can not be less than 2. The number of points can be greater than or equal to the degree, but can’t be less than the degree (an exception constitutes spatial). Spline by Points The degree in it may be greater than the specified number of points.
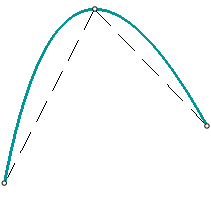
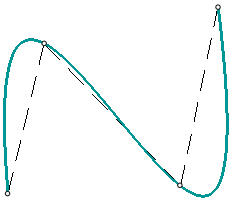
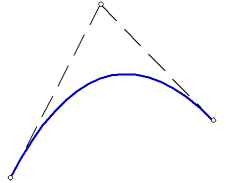
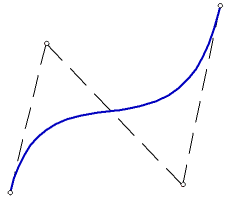
Particular cases of spline curves are shown in the figure.
|
|
|
|
|
|
a) |
b) |
c) |
Particular cases of spline curves (spline by points shown in green, spline by poles in blue):
a) linear curve (number of points – 2, degree – 2, polynomial degree – 1),
b) conical curve (number of points – 3, degree – 3, polynomial degree – 2),
c) cubic curve (number of poles – 4, degree – 4, polynomial degree – 3)
When building a spline surface, you must specify two values that determine the degree in each of its directions: U and V. The specified degree will be followed by isoparametric curves of the corresponding directions.
|
Increasing the spline degree to values greater than 6 is rarely used in practice due to the fact that this will significantly complicate (and therefore slow down) calculations in the operations with curves and surfaces. |
An additional parameter affecting the shape of a spline curve or surface is the weight of each pole. The geometric meaning of this parameter is as follows: the greater the weight of the pole, the closer to it is the curve (surface), i.e. poles with a large weight "attract" the spline stronger than poles with a small weight.
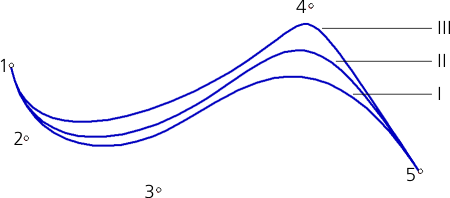
For example, the figure below shows how the shape of a curve changes as the weight of one of the poles increases. Position I of the curve corresponds to the case when all the poles have the weight of 1, position II to the case when pole 4 has the weight of 2, and position III to the case when it has the weight of 6.
|
Influence of the pole weight on the curve shape
|
The shape of the curve is defined not by the absolute weights of the poles, but by the difference between them, i.e. when the change factor of weights of all poles is the same, the shape of the curve does not change. |