KOMPAS-3D v23

Conic curves or curves of conic sections are flat curved lines obtained by intersecting a right circular cone with planes positioned differently relative to the cone's axis.

There are three types of conical sections:

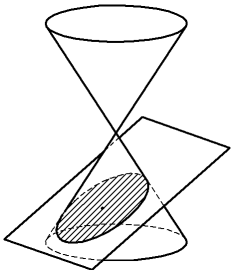
•The cutting plane intersects all generating lines of the cone at the points of a single cavity; the intersection line is a closed curve — ellipse (figure a). A circle as a particular case of an ellipse is obtained when the cutting plane is perpendicular to the axis of the cone. If the plane passes through the vertex of the cone, without intersecting any of its cavities, the circle transforms into a point.

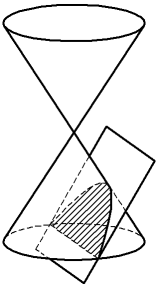
•The cutting plane is parallel to one of the generating lines of the cone; the section will have an open curve that goes to infinity — a parabola, lying entirely within one cavity of the cone (Figure b). If the plane touches the surface of the cone along the generatrix, the parabola transforms into two coincident straight lines.

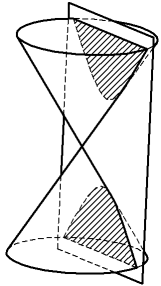
•The cutting plane intersects both cavities of the cone; the line of intersection — the hyperbola — consists of two non-closed parts (branches of the hyperbola) extending into infinity, lying on both cavities of the cone (see figure b). If the cutting plane passes through the axis of the cone, the hyperbola transforms into two intersecting straight lines.

Conical sections: a) ellipse, b) parabola, c) hyperbola

In algebraic terms, conic sections are defined as flat curves whose coordinates in a Cartesian coordinate system satisfy a second-degree equation. In the general form, the equation of all conic sections can be written as follows:

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0

The sign of the discriminant B2 – 4AC determines the type of conic section:

•if the discriminant is less than zero, then it is an ellipse (or point),

•if the discriminant is zero, then this is a parabola (or a straight line),

•if the discriminant is greater than zero, then this is a hyperbola (or a pair of intersecting straight lines).

In a parametric form, a conical curve can be represented by the following equations:

•parabola

x = t

y = a * t2 + b * t + c

−∞ < t < +∞

•hyperbola

•left branch

x = -a * (et + e-t) / 2

y = b * (et - e-t) / 2

-∞ < t < +∞

•right branch

x = a * (et + e-t) / 2

y = b * (et - e-t) / 2

-∞ < t < +∞

•ellipse

x = a * cos (t)

y = b * sin (t)

0 < t < 2π

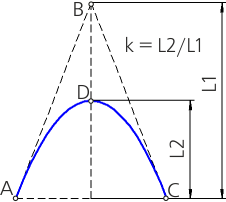
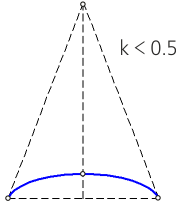
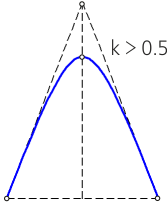
In a graphical plotting, a conic curve can be defined by an arbitrary set of n of its points and m tangents, provided that n + m = 5. One of the most common ways to define a conic curve is by specifying it with two tangents, the points of tangency on them, and a coefficient k (an engineering discriminant).

Coefficient k (engineering discriminant) — the ratio of the part of the median of the triangle ABC located under the curve to the full length of the median of the triangle (figure a).

For a parabola, the value of the coefficient k is equal to 0.5.

For an ellipse, the value of k is greater than 0 but less than 0.5 (0 < k < 0.5).

For a hyperbola, the value of k is greater than 0.5 but less than 1 (0.5 < k < 1).

Relationship between the conic curve type and coefficient value

a) parabola; b) ellipse; c) hyperbola

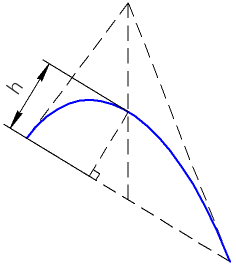
The point of intersection of a conical curve with the median of a triangle can be defined by the height.

Height h of the conical curve — the distance from the point of intersection of the curve with the median of the triangle to the side to which the median is drawn (see figure below).

Height of the conical curve